
本期报告具体信息如下:
时间:2022年10月23日 10:00—11:00



Lecture 6 The Riemann Hypothesis via the generalized von Mangoldt function
黎曼猜想与广义von Mangoldt函数
William Banks
Speaker Bio

William Banks received Bachelor’s degree in California Institute of Technology under Tom M. Apostol from 1982 to 1986, Ph.D degree in Stanford University under Daniel Bump from 1989 to 1994. Prof. Banks worked in University of Carlifornia-Berkeley, Oklahoma State University and became a full professor in University of Missouri-Columbia in 2007. Prof. Banks’ research interest is in analytic number theory, algebraic number theory, representation theory and croptography. Prof. Banks has 120 publications, including Duke Math. J., J. Reine Angew. Math., Compositio Math., Trans. Amer. Math. Soc., Proc. Lond. Math.Soc.
William Banks教授于1982-1986年在加州理工学院取得学士学位,本科导师为Tom M. Apostol教授,1989-1994年在斯坦福大学师从Daniel Bump教授取得博士学位,期间先后在加州大学伯克利分校的MSRI研究所、俄克拉荷马州立大学等地工作,2007年至今任密苏里大学哥伦比亚分校正教授。William Banks教授的研究方向为解析数论、代数数论、表示论和密码学,目前已在Duke Math. J., J. Reine Angew. Math., Compositio Math., Trans. Amer. Math. Soc., Proc. Lond. Math.Soc.等杂志发表论文120篇。
Abstract
Gonek, Graham, and Lee have recently shown that the Riemann Hypothesis can be reformulated in terms of certain asymptotic estimates for twisted sums with von Mangoldt function 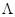 . Building on their ideas, for each
. Building on their ideas, for each 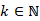 , Saloni Sinha and I have studied twisted sums with the generalized von Mangoldt function
, Saloni Sinha and I have studied twisted sums with the generalized von Mangoldt function
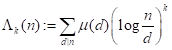
and show that the Riemann Hypothesis is equivalent to the following assertion. For every 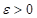 , the estimate
, the estimate
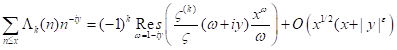
holds uniformly for all 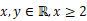 . A similar result is obtained for the function
. A similar result is obtained for the function 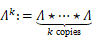 ,
,
the 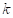 -fold convolution of the von Mangoldt function.
-fold convolution of the von Mangoldt function.
Gonek,Graham和Lee 近期证明黎曼猜想可以被描述为一类von Mangoldt函数的求和问题。以此启发,对于任意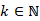 ,我和Soloni Sinha一起研究了广义von Mangoldt函数
,我和Soloni Sinha一起研究了广义von Mangoldt函数
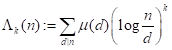
并证明黎曼猜想等价于以下命题:
对于任意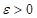 ,
,
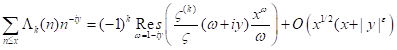
对于任意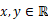 ,
, 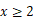 一致成立。
一致成立。